Computational
Earth Physics
  • 4th.CoSy
  • Planetary Temperature
  • CoSy/Life ; CoSy/Liberty
  •  FaceBook ; Twitter 
         ; YouTube ;

    • © Bob Armstrong
      20151223.1229 <
    I apologize for lacking the time to polish this page .
    Post some feedback to motivate my attention .  BA | 20170607.1119 |
    Re : Planetary temperature

    Seeking an executable understanding of the differential in a voxel
    because mapping it over a sphere is rather trivial in an APL like CoSy
    Gravity not "Green House Gas" spectrum  is
    why the bottoms of atmospheres are hotter than their tops .
    But it is not in the energy balance equations .

    It's surprisingly easy to understand
    1. Particles moving "up" in a gravitational field slow down , ie: cool ;

    2. Those moving down speed up , ie: heat . 
    It is only a matter of working out the equations for all matter including atmospheres . 
    Photons themselves heat ( blue shift ) in a gravitational well .
    It is only a matter of working out the equations for all other matter including atmospheres
    For those who truly grok classical physics , it should become clear upon reflection that of the 2 macroscopic forces only asymmetric centripetal GRAVITY can "trap" heat , ie : energy , and in fact must do so to make the equations balance .
    In fact simple computations match atmospheric temperature profiles with undeniable accuracy for all measured planets .  See recently my comments on , eg : Watts Up With That : On #COP21 and the Madness of Crowds .
    ElectroMagnetic spectral effects, constrained by the Divergence Theorem , cannot .

    Al Gore & James Hansen "Green House Gas" demonization of CO2 , the source of carbon to carbon based life , gets an F in physics at a very fundamental level .

    "  ... ever since Kepler proved that the orbits of the planets are ellipses, relations expressible in quantitative form have carried greater weight than those which could be stated only qualitatively."
    F.K. Richtmyer , preface to 1st ed , 1928 , Introduction to Modern Physics , 1942 .



    It doesn't matter how beautiful your theory is, it doesn't matter how smart you are. If it doesn't agree with experiment, it's wrong    . Richard P. Feynman



    I split this discussion from  CoSy's  venerable Global Temperature page to start a ion focused on the actual quantitative audit trail ( h/t Lavoisier  who brought accounting to alchemy transmuting it into chemistry ) from the energy we receive almost totally from the Sun to our observed surface temperature .

     Physics is the mathematical abstraction of  ,
    as an old Hindu buddy would say : ? What is happening ?

    The discussion will be highly prejudiced for the presentation of equations , preferably executable algorithms in some freely available array capable language . This blog is a continuation of the educational effort started at http://climatewiki.org/wiki/Category:Essential_Physics ( archived ) ,  which works out the geometry of the portion of the celestial sphere subtended by the Sun and the Stefan-Boltzmann  T = sb * E ^ % 4  temperature of a gray body . Just this gray body temperature in our orbit , about 278.6 +- 2.3 degrees Kelvin from peri- to ap- helion , explains all but 3% of our estimated mean surface temperature .
    The mystic %100 . Cory Gardner on Gorsuch voting w consensus
    Quantitatively reducing this 3% unexplained variance is the goal .

    The analysis begun in :Essential_Physics was continued with my Heartland presentation , The Basic Basics or How to Calculate the Equilibrium Temperature of a Radiantly Heated Uniformly colored ball , which boils down to

    The equilibrium temperature of a radiantly heated uniformly colored ball is the temperature T
     such that
    dot[ sourceSpectrum ; objSpectrum ]  =  dot[ Planck[ T ] ; objSpectrum ]

    where  objSpectrum  is the absorptivity(=emissivity) spectrum of a object , in this case treating the earth as a uniformly colored ball .  dot[ ; ] is the dot or inner product : the sum across the products of the two curves .

    This can be restated in terms of the Stefan-Boltzmann calculated temperature of a gray body as

    T = Tgray *
        ( dot[ sourceSpectrum ; objSpectrum ] % dot[ Planck[ T ] ; objSpectrum ] ) ^ % 4

    #EqTempEq

    Equilibrium Temperature of a ball
    with an arbitrary uniform absorptivity≡emissivity spectrum
    irradiated by a point source with a given power spectrum
    in K . Conversions to other APLs more than welcome
    /  sb : 5.6704e-008   / ( W % M ^ 2 ) % K ^4
    /  T2Psb : {[ T ] sb * T ^ 4 }
    /  T2Psb..h : " Stefan-boltzmann : Watts % meter ^ 2  from Kelvin Temperature "

    / NB / ( +/ X ) ~ dot[ 1 ; X ]
    / / ( T2Psb T ) ~ dot[ 1 ; Planck T ]
    / / TgrayBody : P2Tsb dot[ 1 ; sourceSpectrum ]

    / Define /
    Absorptivity wrt source / A : dot[ aeSpectrum ; sourceSpectrum ]
    Emissivity wrt Planck / E : dot[ aeSpectrum ; Planck objectTemp ]

    / Then , radiative balance is achieved when /
    ( A * dot[ 1 ; sourceSpectrum ] ) = E * dot[ 1 ; Planck objectTemp ]
    dot[ 1 ; Planck objectTemp ] = ( A % E ) * dot[ 1 ; sourceSpectrum ]

    / And /
    ( T2Psb objectTemp ) = ( A % E ) * dot[ 1 ; sourceSpectrum ]
    / Finally , applying the inverse , P2Tsb , to turn into temperatures /

    ObjTemp = TgrayBody * ( A % E ) ^ % 4
    The next parameter which needs to be added to the computations
    is the gravitational dimension ( parameter ) .
    See Diqusion post below .
    Simple 1D model the GHG paradigm must quantitatively explain :
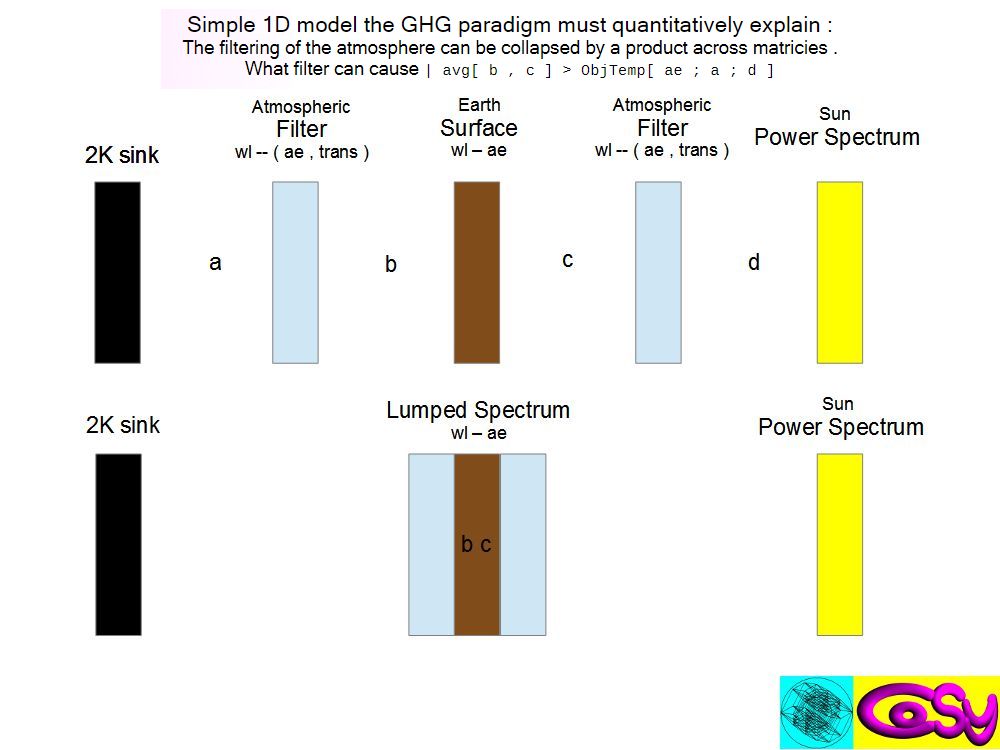
    The filtering of the atmosphere can be collapsed by a product across matricies .
    What filter can cause | avg[ b , c ] > ObjTemp[ ae ; a ; d ]

    1D model

      Scientists Skeptical of Anthropogenic Global Warming
    #RitchiePrize
    The Ritchie Prize
    William Ritchie's 1833 Experiment demonstrating absorption and emission are just two directions thru the same filter
     
    Richtmyer's 1928 description of the Richie's  Experiment simply using hot water


    I'm working to establish a fund for a prize for the best "YouTube" quantitative experimental test of any of the non-optional classical physical computations necessary to get from the Sun's output to our mean surface temperature . | 20170424.1405 |
    Donate to this prize . I'm starting it off with $25


    to CO2isNoEvil on WUWT :
    I'm sorry I don't have more time for this discussion because there is a lot which would be I think generally useful to get clearly communicated . I resonate to such details as "each pixel is 8 bits for most of the satellite channels" . I assume that is for each of some number of spectrally filtered channels ? Your second paragraph reflects any of the problems Roy Spencer describes at http://www.drroyspencer.com/2015/04/version-6-0-of-the-uah-temperature-dataset-released-new-lt-trend-0-11-cdecade/ . I would be quite interested in what your "tools" are built in . APLs can express algorithms over data often orders of magnitude more succinctly and therefore more understandably to the math capable mind than traditional languages . Since in APLs A + B or in 4th.CoSy A B + because it is still at the Forth close to the chip level RPN , A and B
    ... un finished .

     
    • Need to understand / implement  MODTRAN algorithms .

    • Current Status of understanding :

     
    #Disqus
    Willful fools and liars will quickly banned
    comments powered by Disqus
    --
       
    Whole CoSy
    Locations of visitors to this page     		CoSy
     I reserve the right to post all communications I receive or generate to CoSy website for further reflection .
    Contact : Bob Armstrong ; About this page : Feedback ; 719-337-2733
    Coherent Systems / 28124 Highway 67 / Woodland Park , Colorado / 80863-9711 
    /\ /\ Top /\ /\