Category:Essential Physics
From ClimateWiki
It appears to me that they who in proof of any assertion rely simply on the weight of authority, without adducing any argument in support of it, act very absurdly.
Galileo's father , quoted in Richtmyer & Kennard , Introduction to Modern Physics , 1948 .
Planetary temperature is essentially an issue of applied physics . The method of physics is to quantitatively understand geometrical arrangements so simple that they can be experimentally verified . We consider here first , the constraints imposed on a planet's temperature by the constraints on a ball enclosing the planet and its atmosphere . That is , we consider how to calculate the equilibrium temperature of a radiantly heated colored ball . It is worth noting that the mean temperature of a planet is a much simpler problem than the dynamics of its atmosphere just as determining the mean temperature of a volume of gas determined by the Gas Laws is much simpler than determining the details of its internal eddies . The necessary physics is more than a century old .
The most essential results are that the temperature of a planet attributable to the sun is linear with the temperature of the sun and inversely proportional to the square root of its distance from the sun .
Simply adding up the energy ( almost totally from the Sun ) impinging on a point in our orbit explains 97% , all but 10 degrees Celsius , of our temperature . This is the equilibrium temperature of a uniform gray ( flat spectrum ) ball in our orbit ; how light or dark gray does not enter the equation . This is frequently , incorrectly , asserted to be the temperature only of a black ( totally absorptive ) body .
The greenhouse effect is defined to be the difference from this equilibrium due to the difference in correlations between the spectra ( color ) of a ball and its surrounding radiant sources and sinks .
Wikipedia is a good source for much of the relevant basic physics up to
the point at which they are diverted into the "warmist" insistence on a
step function hypothesis for the spectrum of a naked earth . See , for
instance , http://en.wikipedia.org/wiki/Talk:Black_body#Temperature_relation_between_a_planet_and_its_star_-_This_is_wrong
Another excellent resource is C.R. Nave's http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html .
A number of significant questions will be suggested as exercises or points needing elaboration .
[edit] Radiant Heat and Energy
[edit] Radiation and Spectra
Below are the sort of spectra involved in calculating the lumped earth/atmosphere temperature .
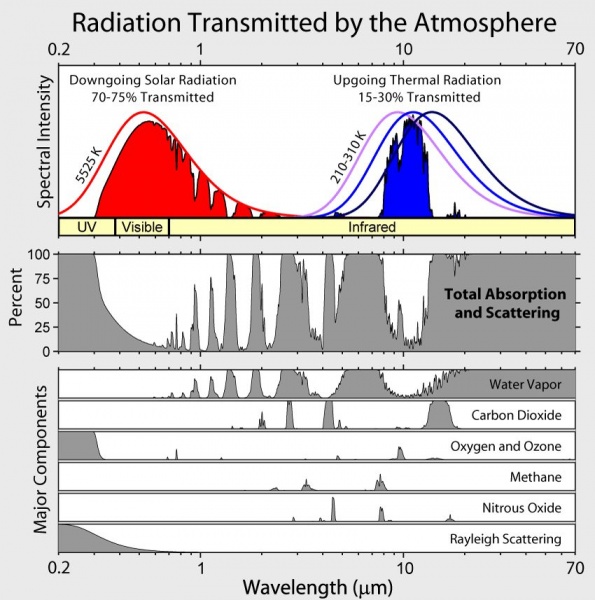
A couple points should be noted about these graphs . First , the Wavelength axis is logarithmic . Second , the Spectral Intensity
curves have been scaled to height . As will be calculated below , the
5525k curve is so enormously larger than the ~ 300k curves that it is
higher than them even at their peak wavelengths .
Our first task below is to show how to calculate the temperatures implied by such radiance and absorption spectra .
[edit] Ritchie's Experiment and Kirchhoff ( Stewart ) law
Considering first opaque bodies , a surface may either absorb radiant energy converting it to thermal energy , or reflect it .
We will call the proportion absorbed , the grayvalue, gv , ranging from 1 for a perfect black body to 0 for a perfectly white , reflective , body .
By 1860 , the crucial , but poorly understood by today's "climate scientists" , fact that a good absorber is a good emitter & vice versa had been codified by the great Gustav Kirchhoff and similarly by the lesser known Balfour Stewart .
The observational foundation of Kirchhoff's law was an elegant experiment a generation earlier by William Ritchie .
I've seen a better presentation of it than the image below
but have not been able to find it again . This image is extracted from Demonstration Experiments in Physics by Richard Manliffe Sutton , 1938 . I'd appreciate a better source if someone finds one .
I find it notable that this law can be demonstrated with just the difference between hot and room temperature water .
I've added the neutral labels A and B because the implications of this experiment are far more general than just the extreme absorptive and reflective surfaces described . The brilliance of Ritchie's set up is that he effectively commutes absorptivity ( the transduction of radiant to material thermal energy ) and emissivity ( the transduction of thermal to radiant energy ) with respect to temperature .
-
( ( A B ) T0 ) = ( ( B A ) T0 )
-
[edit] Stefan-Boltzmann law
The Stefan-Boltzmann law is a simple equation which states that the Power ( energy per unit time ) radiated by a body is proportional to its Temperature raised to the 4th power multiplied by the stefan-boltzmann constant derived from fundamentals which converts degrees Kelvin to watts per square meter .
| Stefan Boltzmann Law |
||||||||||
|
||||||||||
The energy flows per unit area can then be summed up over surfaces . We will also need the inverse function to convert back from power to temperature . Note that the sb constant falls out when we make a round trip from temperature to temperature .
Since computations in energy are linear , the net rate of energy transfer between two objects is the simple difference of each of their individual rates , ie , {[ T0 ; T1 ] -/ T2Psb' ( T0 ; T1 ) } . The net energy flow , and therefore heat flow , is from whichever is warmer to whichever is cooler . No mystery ( except that { sb * T ^ 4 } bit solved more than a century ago , itself ) .
In classical physics fashion , one can determine the power density , and therefore temperature , at a point by simply integrating ( summing ) the energy flux over its surrounding sphere , {[ T ; s ] +/ Psb T @ s } , where s is a partition of the sphere . As a Gaussian surface I'm sure tons of related implications can immediately be made for spheres in place of points .
[edit] Orbital geometry
Here are the radius of the sun and our distance from it in meters . mean is the mean of our aphelion and perihelion distances .
- : SunSpecs[ `radius `ap `peri `mean ] : 6.96e+008 5.234958e-6 5.596861e-6 5.411374e-6
| radius | ap | peri | mean |
| 6.96e+008 | 1.520977e+011 | 1.4709807e+011 | 1.4959789e+011 |
Over geological periods , the eccentricity of our orbit changes as does the tilt of our axis of rotation relative to our orbit . These have measurable effects on our mean temperature ( and global climate ) . See , for instance , the work of Nicola Scafetta . Currently we are at perihelion about January 3 , about 2 weeks after the northern hemisphere's winter solstice .
The "temperature" of a point in space may be calculated by adding up the radiant energy flows impinging from all directions around it . Almost all our energy comes from the sun , so the first task is to calculate the portion of the total celestial sphere around us it subtends . The solid angle subtended by a disk is simply its area , pi * R ^ 2 , projected onto a sphere of radius 1 , that is dividing it by its distance , D , squared ( because it's an area ) . The unit sphere has a total area of 4 * pi . So the portion of the total sphere covered by a disk is simply its solid angle divided by 4 * pi .
| Portion of sphere covered by disk of radius R at distance D | |||||||||||
|
|||||||||||
So , the portions of the celestial sphere covered by the sun at ap- and peri-helion and mean distances are :
- : SunSfrPrt[ `ap `peri `mean ] : PoS . SunSpecs @' ( `radius ; `ap `peri `mean )
| ap | peri | mean |
| 5.234958e-6 | 5.596861e-6 | 5.411374e-6 |
Our planet is heated by just five millionths of the total sky .
[edit] Calculating the Temperature of a radiantly heated Gray Ball
Now that we have the function for the conversion of thermal energy to radiant flux and the portion of the celestial sphere covered by the sun we can we can calculate the total energy impinging upon a point in our orbit . ( OT : The reason the sun appears uniform across its disk is Lambert's cosine law . )
Using SunSfrPrt.mean calculated above , we can make a table of the observed sun and cosmic background temperatures and portions of the celestial sphere they cover .
- SunTemp : 5778 ; CBR : 3
- : TP : ( SunTemp , CBR ; SunSfrPrt.mean , 1 - SunSfrPrt.mean )
| 5778 | 5.411374e-006 |
| 3 | 0.9999946 |
To show that the Stefan-Boltzmann constant , or any other just drops out
of the overall equation , here are both the naked temperatures raised
to the 4th , and the actual watts per square meter given by T2Psb :
- : T0 : ( ( TR 0 ) ^ 4 ; T2Psb TR 0 )
| 1.114577e+15 | 6.320098e+7 |
| 81 | 4.593024e-6 |
Now we multiply each column by the portions in TP :
- : r : ( TP 1 ) */: T0
| 6.031394e+9 | 342.0042 |
| 80.99956 | 4.592999e-6 |
Now we sum across the partitions of the sphere :
- : r : +/' r
| 6.031394e+9 | 342.0042 |
It's clear the 3 kelvin cosmic adds up to nothing , altho it represents
all but 5 millionths of the sky . However , if you entered a background
of , eg , 100 kelvin you'd start seeing it having an effect .
Now converting back to temperature we have :
- ( ( r 0 ) ^ % 4 ; P2Tsb r 1 )
| 278.6791 | 278.6791 |
This approximately 279 kelvin commonly asserted to be the temperature of
a black body in our orbit . Note that throwing in any grayvalue , gv , (
other than 0 ) will drop out of the computation just like sb . Thus
this is the temperature for any uniformly gray ball however dark or
light .
We are about 10 degrees warmer than this .
To summarize the computation into one function on any table , TP , of partition of temperatures over the sphere :
- PointTemp : {[ TP ] ( +/ ( TP 1 ) * ( TP 0 ) ^ 4 ) ^ % 4 }
| Temperature of a radiantly heated gray ball |
||||||
|
||||||
[edit] Planck radiation function
Planckf : {[ f ; T ] ( ( 2 * h * f ^ 3 ) % c ^ 2 ) % ( _exp ( h * f ) % Boltz * T ) - 1 }
Planckl : {[ l ; T ] ( 2 * h * c ^ 2 ) % l ^ 5 ) % ( _exp ( h * c ) % l * Boltz * T ) - 1 }
[edit] Calculating the Temperature of a radiantly heated Colored Ball
[edit] Semi-transparent ball with inclusions
[edit] Beer–Lambert law
[edit] Vertical Structure of Atmosphere
[edit] Atmospheric Convection
[edit] Other sources of heat
While much smaller than the radiant energy from the sun , there are several other sources of energy to the earth's surface , some of which may be locally significant , which must be considered in a complete audit .
[edit] Geothermal
[edit] Man Made
Particularly around urban areas , the gigawatts of energy released from fossil and nuclear fuels , not just changes in spectrum and terrain can be significant .
[edit] Solar and Other Particulate
Some amount of energy impinges on the earth in the form of kinetic particles in form of the Solar Wind and meteors .
[edit] CO2 & Atmosphere
[edit] CO2 respiratory cycle
The initial content of this page is based on the analysis at http://cosy.com/Science/TemperatureOfGrayBalls.htm . In the spirit of Donald T Campbell's Fish Scale Model of collective Omniscience this site needs the knowledges of more minds . However , the purpose of this site is to nail down the physics . Thus only data and explicit experimentally verified or verifiable quantitative , computable assertions , ie , equations and their explanations and proofs are admissible . As various intervals of understanding are accreted , we intend to create tables of vocabulary implementing those relationships in various programming languages so individuals can "play" with the concepts themselves .
The executable notation used by me here is Arthur Whitney's APL evolute K' . Translations into more accessible languages are most welcome .
Please post comments and suggested clarifications or additions to the discussion page for "peer review" before posting to this page . --Bob 15:47, 15 July 2011 (UTC)
This category currently contains no pages or media.
