It is commonly asserted that the basic physics of planetary temperature is well understood. However, it is surprisingly difficult to find any exposition of that basic physics. This lack contributes to the most egregious impossibilities being touted as ultimate horrors we might face if we don't mend our ways. On the skeptic side, it has even been claimed that the notion of a planetary mean is meaningless. I present below my current understanding. I welcome review and, indeed, co-authorship with someone with more established credentials.

I originally started working on this around Thanksgiving 2008 and hoped to propose talking about it at the Heartland Institute's March 2009 climate conference , but clearly , it's too late for that . I find that altho my master's thesis had integrals which filled a page , having spent an adulthood in the arrays of the most powerful languages for modeling actual finite data , I'm terminally inept at expressing ideas in traditional maths notation . I have , however , instantiated the basic formulas for anisotropically irradiated anisotropically shaded gray balls in the rather obscure APL evolute K.  I believe , tho , that the succinct model can be understood and translated into common array capable languages by anyone familiar with any such language . ( see Forum for translations to J and Dyalog APL . ) 

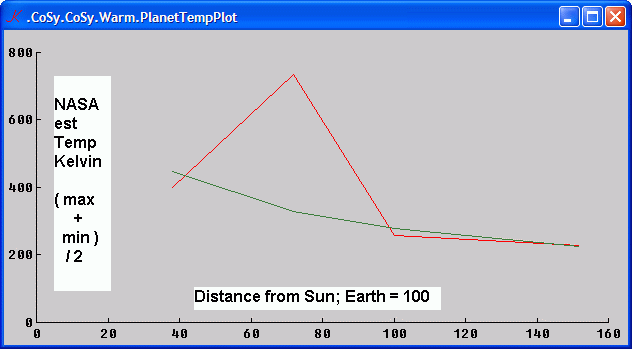
I will not consider fluid motion of the atmosphere because our interest is with mean temperature averaged over the sphere over time. Our interest is in the constraints on the temperature of radiantly heated balls like our earth, in a sense looking from the outside rather than looking up at the complexities of the atmosphere.

The fundamental law whose most superficial application explains all but at most a couple of percent of the earth's temperature is the Stefan-Boltzmann law. Applying this basic law for black bodies to the surface temperature of the sun and the solid angle it makes in the sky explains the mean temperatures of each of the inner planets, except for Venus, quite closely as shown in the graph [0] .

The Stefan-Boltzmann law is a simple equation with a complicated constant derived from fundamentals which states that the Power radiated by a body is its Emissivity times the stefan-boltzmann constant times its Temperature raised to the 4th power.

The "Black Body" Wikipedia page was the first place I saw the derivation of the Earth's temperature from the Sun's based on this equation. It simply equates the power radiated by the sun and intercepted by the disk of the earth with the power radiated by the earth in all directions:[1]

Canceling terms and rearranging a little, we get

        ( ( Ts ^ 4 ) * ( Rs ^ 2 ) % ( 4 * D ^ 2 ) ) = ( Te ^ 4 )       | e2 |

and taking 4th roots:

        Te = ( ( Rs % 2 * D ) ^ % 2 ) * Ts       | e3 |

or to express as a function :

        Trd : {[ R ; D ] ( ( R % D ) % 2 ) ^ % 2 }       | e4 |

Note that the radius of the Earth has dropped out; thus a point is equivalent to a sphere, and only the solid angle subtended by the Sun matters. 

Plugging in values of 6.96e8 and 1.496e11 meters for the radius of the Sun and the distance from the Earth to the Sun gives the result th at the temperature of a black body in Earth's orbit has a temperature of about 0.04823 the surface temperature of the Sun . This is the computation which produces the green line in the plot above.

Note that given that the SolidAngle subtended by the a disk of radius R at distance D is 

    SAd : {[ RD ]  pi * %/ RD ^ 2 } 

 , equation e2 can be rewritten 

        ( ( Ts ^ 4 ) *  SAs % ( 4 * pi )  ) = ( Te ^ 4 )       | e5 |

Gray Bodies

But, of course, the real planets are not black. For a "gray" body, there is an associated parameter Emissivity, constant across the spectrum, which like a gray filter in front of a radiating black body, uniformly reduces the power at each frequency from what would be expected from a black body. There is a complementary parameter Absorptivity, ranging from black to totally reflective, which quantifies the tendency of a substance to absorb radiant energy.

150 years ago in 1859, Gustav Kirchhoff realized that at equilibrium, the emissivity of an object must equal its absorptivity, E = A . Thus equation e2 above would become

        (  Ae  *  ( Ts ^ 4 ) * ( Rs ^ 2 ) % ( 4 * D ^ 2 )  )  =  (  Ee  * Te ^ 4 )       | e5 |

with terms Ae * and Ee * added to the left and right sides for the Absorptivity and Emissivity of the earth respectively. But, by Kirchoff, these terms cancel out at equilibrium.[2] In the middle of 2008, the Wikipedia Black Body page was modified adding the Ae to the left side of this equation but failing to add Ee to the right side.

Judging from Wikipedia references, this explanation of the greenhouse effect seems to be common in texts on global warming. But this explanation is simply wrong. If it were the case, one would expect a ball coated with Magnesium Oxide with an albedo of about 0.9 to come to an equilibrium temperature of about -120c in a vacuum bottle sitting in room temperature surroundings. Venus has the highest reflectivity of all the inner planets, about 0.75 . This would imply a temperature about 30% below the calculated black body temperature for its orbit, or about 233k versus 328k . However, of course, Venus is radiating energy at a temperature of about 735k, both on the side facing and away from the Sun -- and its day is slightly longer than its year. The most heating this greenhouse theory could predict is raising the temperature back to the black body temperature. No "runaway" effect could raise the temperature beyond that. On the other hand, according to this theory, as snow with an albedo which can be nearly as high as MgO covered the continents during the ice ages, the Earth should have spiraled down to a permanent snowball. That it didn't is one of the first facts which made me question the AGW orthodoxy. It is notable that, so far as I know, there is no laboratory demonstration of this supposed phenomenon.

From this point on , I will use actual expressions from my K implementation of the Stefan-Boltzmann Law for the simple case of a point in its surrounding sphere . The equilibrium temperature of a ball will vary if the absorptivity/emissivity parameter is different in directions with different temperatures.  We can express this as a function on 3 vectors and a scalar : a partition of the celestial sphere, SfeerPart , the temperature of each partition of the celestial sphere , Tcs , the absorptivity/emissivity of each partitian , AE , and the temperature of the ball considered to be uniform , Tp . ( This is the parameter upon which it is a point . ) We will just deal with a partition of the sphere into ( SunDisk  ; DaySide ; NightSide )  . 

Other than the disk of the sun , the celestial sphere presents the approximately 3 degree K microwave background radiation . We'll include it altho taken to the 4th power it ends up being quite negligable .

Finally ,  there is the absorptivity/emissivity , the grayness , of each sphere partition . We will look at several cases starting with all black .

[1] My notation is informed by an adulthood living in APL languages. The rational is summarized here . Perhaps the only non obvious symbol is % for division and reciprocal. In APL languages f/ can be read as "f across", for instance +/  is "sum".  "

[2] I've heard complaints that the Earth and Sun are not in equilibrium, but I believe that over a cycle, like Earth's yearly cycle, it can be proved that for a conservative quantity like energy, the outcome is equivalent.
I have seen it pointed out that Kirchhoff's equating of absorption and emission only applies at equilibrium. However absorption and emission spectra are generally rather constant for a substance over a given physical state. For instance, it is when water changes to snow that it's albedo changes drastically.