/(/ Renamed from NL0506 20070930 / sun.jun.20050619.151131 /)/
4th.CoSy
On those weekends I have stolen time to work on 4th.CoSy , I have made progress
only possible in FORTH . I have never worked in a non-interpretive language
since FORTRAN days ( before meeting APL around `75 ) and cannot imagine working
in a traditional compiling environment . Building structures directly in the
machine's static address space with FORTH is clumsy enough .
It's very hard to get across why language creation is so
foundational a pursuit . I have not been very successful at conveying
an understanding of most of the consequential things I've done in my
life , especially before the fact . That's a reason why I have on a
couple of occasions done things whose geometric purity is self evident
.
The nature of 4th.CoSy .
My description below reflects the current state of 4th.CoSy . Some
details , like the structure of the header of objects , may change .
The implementation of 4th.CoSy is as minimalistic as I can conceive .
I believe that simplicity of rules comes from simplicity of code , so
4th.CoSy "theory" comes naturally from its implementation as opposed to the
APL tradition of forcing grand notions into reality .
All counting starts with 0 because 0 is the 1st number . I will
generally follow the convention of using ordinals 1st , 2nd ...
corresponding to
" 1 take " ... . This is a constant conundrum tho . |
A good image for the structure is perhaps a tree or a bush , each
branch having any number of branches , leaves , flowers , or other
things on it . More formally , everything is a list of 0 or more items
which may themselves be lists or something else . If it is a 4th.CoSy
list , its 1st cell ( 32 bit word ) is a 0 . That "something else" is
essentially open-ended and what exactly the object may be is given by
it's type which is stored in that 1st cell . Generic 4th.CoSy objects
have a header , currently of 4 cells as shown below .
| t y p e | count ( # of items ) | bits % item | reference count | meta | <--- body of object ---> |
Note that all objects created so far have a count so are set up to be
lists themselves which most of the items created so far are - lists of
integers , strings of text , symbols - which are just specialized
strings .
All objects in 4th.CoSy are dynamically created in virtual memory ( allocated ) and destroyed
( freed ) as needed . That reference count keeps track of whether anything is using the object . |
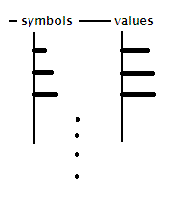As I said , everything in 4th.CoSy is a tree or a leaf . The language
itself , the dictionary , is a tree . It's a tree with currently 2
branches ; the first is a list of words ( symbols ) in the vocabulary
and the second , a matching list of the values ( definitions ) of those
words . Following Charles Moore's brilliant use of whitespace ( blanks
) as the prime delimiter , words can be any non-blank string of
characters as in FORTH . The values can be any 4th.CoSy object ,
including , of course , 4th.CoSy lists .
[ 20070930 | have added a third "attibute" column ala K ala some Lisps
| 20071101 | poor notion . will replace with cell in header ]
VOCABULARY
The power of APLs comes from their vocabulary to apply functions (
verbs ) to lists . Many of the earliest words I have created in FORTH ,
even to implement the parsing and interpreter yet to come are "APL"
words . Much of this discussion will resonate more with APLers than
"outsiders" . Note the examples are FORTH "parse a word , do it" syntax because they are in fact at this point in time all executing in FORTH .
An example of how transparent to the machine 4th.CoSy is is given by the definition of @ which is machine code :
: @ inline{ 8b 00 } ;inline ( a -- n )
| get the contents n of cell at address a
see @
005FCECB 8B 00 mov eax,[eax]
005FCECD C3 ret
|
- i# The number of items in an object is , as shown above , stored the 2nd cell of the header so the FORTH is simply
: i# cell + @ ; name changed to avoid conflict with FORTH # ) .
- i@ and i! Index fetch and store . All indexing is is modulo . That is , indexing wraps around so that
Obj i# i@ grabs the same item as Obj 0 i@ , and Obj -1 i@ grabs the last item , Obj i# 1- i@ .
- each in various forms and across .
( At this level in FORTH , there isn't the generic covering of
functions specific to each data type like byte or integer so multiple
forms are needed . ) These "operators" ( adverbs ) can be implemented , tho in a primitive form , in FORTH because FORTH's
' function returns the address of a word making it easy to pass that pointer to a function which then calls execute
to actually execute it . I plan to retain this style of passing the
pointers to words , generally their symbolic names , to functions which
may take functions as arguments . Thus , APLs distinctions between
functions ( verbs ) and operators ( adverbs ) and possibly higher order
constructs becomes rather open , arbitrary , and extensible .
- take , APL's "rho" . Consistent with the modulo indexing ,
List n take replicates the items of List cyclically to length n .
- & Arthur Whitney's "where"
function . For each item of its integer argument , return n
replications of corresponding index . This is one of those APLish
definitions which seem terminally inscrutable , but the normal use is
just to extract the indices of 1s in boolean lists of 0s and 1s . It's
just that the more general definition is just about as easy to write ,
and does have some very subtle uses .
- _ Arthur Whitney's "cut" function .
Splits or partitions a list into sublists at a set of indices . If
there is just one index , it's the same as APL's "drop" .
- ? A generalization of Whitney's
"find" and APL's dyadic "iota" which return the index of the first item
in the left argument matching the right argument . ? in CoSy is an operator , list fn ? item which returns the first index in list where { fn item } is true . If not found , returns nil .
- general function application
Generally , arguments are "taken" to the length of the longer for
application of "atomic" functions . This is a generalization of APL's
"scalar" extension .
|
