Last night I finally had time
to reply to the first 19 or so replies to my request for comments on my
implementation of the basic Stefan-Boltzmann/Kirchhoff
equation for radiantly heated spheres . Rather than burden
everybody with all the posts and my comments , I have once again posted
them to the
topic on my forum
. I thank everyone for the unexpected amount of feedback . I feel
overall it illustrates the pathetic state of the understanding of the
basic physics involved , even within the realist
camp . This
ignorance cries out for the simple experiments which would put much of
these arguments to rest .
Perhaps the most substantive comments came from Howard Hayden . I think
we are much closer together in our understanding than he thinks . He
seems to think I'm saying more than I am . I'll repeat that I have only
implemented the scalar , gray body absorptivity/emissivity parameter
model . I am working on the couple of lines required to implement the
full spectrum version . But I already spend far more time on this than
is conducive to my economic well being .
Apparently a lot of people have made lots of incorrect implementations
of Stefan-Boltzmann which produce ridiculous predictions . My correct
implementation gives a temperature of about 278k for a uniform gray
ball at this distance from a 5772k sun . I believe that's within a few
percent of commonly observed mean values .
Essentially the only question I am addressing with this cut is which of
the following formulas for a gray ball is correct :
The ubiquitous , eg , on the Wikipedia black body and Stefan-Boltzmann
pages , and apparently a lot of texts :
( EarthAbsorptivity
* SunSolidAngle *
TempSun ^ 4 )
= ( TempEarth ^ 4 )
or
( EarthAbsorptivity
* SunSolidAngle *
TempSun ^ 4 )
= ( EarthEmissivity * TempEarth ^ 4 )
where for a gray ball EarthAbsorptivity
and EarthEmissivity are equal
. SunSolidAngle is
expressed as a fraction of the total sky .
The first equation produces a result EarthAbsorptivity^0.25
lower than the second , about 253k for the earth
. From there on , all I see is word waving to fill in that gap and
claim there is no upside limit to the planet's temperature .
Can we eliminate one of these two equations ? Can there be
any claim
to this being a scientific pursuit if we can't ?
--
-- Bob
Armstrong -- CoSy.com
--
719-337-2733 --
I reserve
the right to post all
communications
I receive or generate to CoSy website for further reflection .
[ BA comments ]
Well , I'm glad to be getting light shed on this
timely bit of physics . Here are my comments on the stream of emails
I've received .
Alan Siddons 8/3/2009 14:19 :
By the way: "a null hypothesis that gray bodies absorb as gray bodies
but emit as black bodies" says it very succinctly. Wish I'd thought of
those words myself!
Howard Hayden 8/3/2009 15:51 :
Time to be careful !!
The absorptivity and emission coefficients are identical at each
wavelength; however this does not mean that the coefficients at (say)
550 nm and at 15,000 nm are the same. It is perfectly
possible for a (gray) body to absorb sunlight poorly (centered at
around 550 nm) but to emit IR well (centered at 10 nm, corresponding to
288 K). Indeed, it's the case that plain old white snow has
an emission coefficient very near 1.0. Funny that snow is a
good "blackbody", but that's the way it is. Almost everything
except shiny metals emits well in the IR region.
The only definition of "gray" I can make sense of
is a totally flat spectrum for all frequencies . That is certainly what
is
implied by using a scalar value for AE
. As I have said , I'm working on implementing the Planck function , BB[
f ; T ] , so that each item in AE
will be a spectrum to be multiplied by BB[ ; T ] to
calculate the effect of color . ( NB : the K
language , and perhaps J , has the useful feature
that eliding a parameter essentially "projects" the function onto that
parameter . )
Alan Siddons 8/3/2009 17:33 :
As Brian has lectured me, though, emissivity for real objects also has
a directional component. Change your angle of view and you’re likely to
get a different emissivity reading. Another complication is albedo
(reflectivity), which varies by direction as well. I suppose that’s one
reason why "bond albedo" was devised, given that Saturn’s frosty moon
Enceladus has a visual albedo above unity, which would imply that it
can’t be radiatively heated at ALL! In some sense it seems to me that
if you want to determine a real body’s temperature response to
sunlight, there’s nothing like a simple thermometer...
Again , I'd refer to the actual formula for what is actually
implied . The function is
PgrayBall
: { +/ AE * SfeerPart * Psb x } / total
radiated power from shaded gray ball
where my perhaps unfortunately named SfeerPart
is the only parameter which induces any specific geometry . And it
induces spherical geometry only in that it is composed of a partition
of the celestial sphere .
:
SfeerPart : ( ( ( :: ; pi2 - ) .\: SAsun ) , pi2 ) %
pi4 />/ 5.4113742e-006 0.49999459
0.5
where SAsun is the solid angle subtended
by the sun .
AE then assigns a gray value to each point on that
integrating sphere . An integral over the hemisphere normal to each
direction would be more precise , but I would bet that it would be hard
to construct an angular distribution of albedo which would
significantly the results .
All this aside, however, the point that needs stressing is
that there’s
a necessary dislocation between irradiance and temperature on a
spherical surface.
Since the time when Fourier formulated
the heat conduction equation, a non-linear boundary condition
describing radiative transfer of a globe with a Sun-side and a dark
side has never belonged to the family of solvable heat conduction
problems, even in the case of a non-rotating globe. — Gerlich and
Tscheuschner
Dr Hayden mentioned this to me when we met at the 1st
Heartland conference . While I appreciate the elegance of an analytical
answer , for good or ill from a modern programmer's perspective
it's a big "so what" . What matters is if the error function converges
uniquely . And integrals over T^4 very definitely
do .
That is, our spherical earth can NOT be regarded as a flat plate
receiving an "average irradiance" in the first place. A flat plate
model gives you a 255 K estimate. But a half-and-half model (one round
hemisphere sunlit, the other one dark) gives you 153 K at best!
Incorporating a meridional solar zenith irradiance will yield yet
another figure. In other words, the very assumption that you can derive
a temperature from the average irradiance on a sphere is wrong. Among
prominent AGW skeptics, only Vincent Gray and (to a lesser extent)
Richard Courtney understand that the Kiehl-Trenberth radiation model is
inherently invalid, therefore. On a mathematical basis alone, average
temperature does not conform to average irradiance due to the 4th power
relationship. Still "more" impossible is trying to make those two
parameters get along on a non-blackbody sphere. Bottom line: the
widely-cited average earth temperature of 255 Kelvin is bogus.
I'm not clear on just how you are doing your calculations ,
but
my PgrayBall matches the value
calculated by the equation on the Wikipedia Black Body page
before it was screwed up . And both give temperature ratios of
about 0.0478 and 0.0486 for an object at aphelion and
perihelion in our orbit relative to that of the sun . These give mean
temperatures of about 276.4 and 281.0 for a temperature for the sun of
5778 . That leaves at most a few percent error to be explained . The
perihelion - aphelion variation is an obvious effect to be looked for
in the historical data to test the computation .
Howard
Hayden 8/3/2009 18:31 :
Alan:
Right. The moon, for example, has highly directional
reflectivity; the light from the moon is down by nearly 50% one day
after or one day before full moon.
G & T are perfectly correct that you should not treat a sphere
as a flat plate. They also comment correctly that the average
temperature is a meaningless quantity.
So , is it meaningless to assign a mean temperature to every
astronomical body ? I think this is a
total cop out .
G & T are perfectly incorrect in saying that a body cannot
radiate IR to a hotter body. (At least, that's the way I read
what they said. Correct me if I'm wrong.) We
receive lots of microwave radiation from outer space that is at 2.8
degrees above absolute zero. It has a minuscule, but
non-zero, warming effect on the earth.
Correct . I have the cosmic background radiation at 3k in my
calculations , but with
that
T^4 relationship , the 0.9999946 of the
sky at that temperature makes little difference .
But all of that is beside the point that I was
making. I was commenting on this
sentence: "I'm left astounded that such a howler as
having as
a null hypothesis that gray bodies absorb as gray bodies but emit as
black bodies could get past any competent peer review ."
It
is incorrect to equate the absorptivity at one wavelength to the
emissivity at another wavelength.
We must be very careful, because the warmers are wont to jump onto
every misplaced comma to demonstrate that "deniers" are all a bunch of
incompetents.
Again , that's why I am working on "unfolding" AE
across spectra . But I won't be able to get to it til late this month .
And then , I will be looking for a convenient source of all relevant
spectra .
Alan Siddons 8/3/2009 21:08 :
It
is incorrect to equate the absorptivity at one wavelength to the
emissivity at another wavelength.
Absolutely. But look at
it this way while playing with simplistic climatology assumptions. Say
a body is 0.7 absorptive, i.e., it reflects 30% of the incident light.
Whereas 1000 W/m² would raise a blackbody to 364 K, then, this body
will absorb 700 and reach 333. Fine so far. Maybe. Ah, but
absorptivity equals emissivity, remember, and climate models
make no wavelength distinctions. It's watts per square meter from
beginning to end, which is the ONLY factor you have to worry
about when a blackbody is involved. So yes, a blackbody at 333
K will emit 700 W/m². But a 0.7 emissive body AT THE
SAME TEMPERATURE will radiate 490!
What I’m getting at is
that the famous "255 K" earth estimate simply regards the target as a
uniform, semi-reflective plate and divides net radiation by
four to compensate for a sphere’s greater surface area. Yet many
different substances with different emissivities are creating that 30%
reflection. Look at water alone.
- http://www.monarchserver.com/TableofEmissivity.pdf
- http://www.ib.cnea.gov.ar/~experim2/Cosas/omega/emisivity.htm
Keeping in mind that
the earth is 70% covered with water and that
laboratory-derived figures tend to be higher than in the real world,
can you say with fair assurance that a 333 K graybody
will radiate at the same intensity as a blackbody? Will a 288 K
"average earth" actually radiate 390 W/m²?
Again , I'd like to stress that all
I am demonstrating with the monocromatic implementation is that albedo
, uncorrelated with the sources or sinks of heat doesn't
matter . And it is a total howler to use equations which simply ignore
Kirchhoff's insight .
Now for the more
difficult stuff.
G&T
are perfectly incorrect in saying that a body cannot radiate
IR to a hotter body.
Aye, there’s the rub.
It is more precise to say that a cooler body radiates IR toward a hotter body.
But does this radiation raise the hotter body’s temperature? No,
because it can’t. I realize that such an assertion is
controversial, but the second law of thermodynamics wouldn’t make sense
otherwise. Here's how professor M. Quinn Brewster, for instance,
expresses it in his book Thermal Radiative Transfer and
Properties:
Like conduction,
thermal energy is in harmony with the second law of thermodynamics such
that, in the absence of work, thermal energy is radiated spontaneously
from higher temperature to lower temperature matter.
FROM
and TO.
To frame that a bit
more tightly, if radiation TO a body is less than the radiation FROM
that body, this energy does not raise that body’s temperature. If
radiation to a body is greater than radiation from that body, this
energy does raise that body’s temperature. Conductive and radiative
heat transfer obey the same rule, that of thermal energy flowing to a
zone of lesser energy. That is my own formulation of the second law as
it applies to radiative heat transfer.
Were a cool body to
lend heat to a warm body, as a warm body lends heat to a cool body,
then logically both would be heating each other. So when would this
reciprocal heating process STOP? Fact is, it wouldn’t. A hot radiating
ball suspended inside a cooler (and well-insulated) shell, for example,
would exchange heat between them infinitely, both of their temperatures
mounting minute by minute.
In real-life, however,
the hot ball will transfer heat to the cool shell until both of their
temperatures are the same. Just as in a conductive transfer context,
the cooler shell contributes nothing of its own; it is merely a
receiver. Because transfer literally means transfer: the heat flows
only one way, from greater to lesser. So the shell gains at the ball’s
expense. A transfer is not an exchange. It is from and to.
But here’s the upshot:
If I am wrong, simply prove it! I’ve read about "reciprocal heat
transfer via radiation" till my eyes bug out of their sockets. Yet no
formula in any physics textbook describes this alleged phenomenon, as
Gerlich and Tscheuschner have also mentioned.
Question: With a
radiative input of 1000 watts per square meter and an output of 50%
(meaning 50% back-radiation from a re-emitter), what temperature will a
blackbody reach?
There SHOULD be an
answer to such an elementary question. But there isn’t. The formula is
missing from textbooks because the phenomenon itself does not
exist. Neither conductively nor radiatively can a cool body
transfer heat to a warmer body. So says me. But if I’m wrong, show me.
Actually , what you can't do is add the temperature
of layers of an object heated by a source to
subseqent layers because the energy in those layers has come from that
source . All it can do is add back the energy it has absorbed .
However , this is another example of the common
failure I see to consider that we are a sphere heated by only 5
millions of the sky . In all other directions , we are the hotter body
. Here's what the equation gives for a uniform blackbody with
background temperatures of
3k , 0k , and 100k
:
SfeerPart : ( ( ( :: ; pi2 - ) .\: SAsun ) , pi2 ) % pi4 />/
5.411374e-006 0.4999946 0.5
AE : 1 1 1 ; Tcs : 5778 3
3.0 ; ?[ Tdif ; 0.0 ; 300. ]
/>/ 278.6791
AE : 1 1 1 ; Tcs : 5778 0
0.0
; ?[ Tdif ; 0.0 ; 300. ] />/ 278.6791
AE : 1 1 1 ; Tcs : 5778 100 100.0 ; ?[
Tdif ; 0.0 ;
300. ] />/ 279.8271
As I said above , the 3k background becomes totally insignificant when
raised to the 4th . However , if the background temperature were 100k
in all directions , it would raise the temperature of the earth about
1.15 degrees .
Energy is always exchanged in both directions but the net is always
from hotter to colder . That the cooler radiates toward the warmer is
reflected in the fact that the rate of energy flow is ( Th - Tc ) ^4
. The closer in temperature the source and sink , the slower the rate
of convergence of temperature .
Howard
Hayden 8/3/2009 22:12 :
Alan:
"Absolutely. But look at it this way while playing ..."
That's changing the subject.
I'm simply saying DO NOT support strong cases with incorrect
arguments. Remove the incorrect "howler" sentence and get on
with the correct argument.
"But does this radiation raise the hotter body’s temperature? No,
because it can’t...."
Wrong. Do you seriously
believe that the background microwave radiation (as trivial as it is)
has precisely the same effect on the earth's temperature as if the
background were at absolute zero? Do you believe that if the
temperature of outer space were suddenly warmed to 200 K that it would
not warm the earth?
Here's the calculation :
AE
: 1 1 1 ;
Tcs : 5778 200 200.0 ; ?[
Tdif ; 0.0 ;
300. ] />/ 295.5635
The point, from a 2nd-law point of view, has to do with net radiation
flow. Remember, the thing (aside from emissivity
considerations) that determines the amount of radiation is the
temperature. A cold body does not fail to radiate simply
because a warm body is near, and the warm body does not fail to absorb
the radiation that impinges upon it. There is no net heat
flow from colder to hotter. This is not a violation of the
2nd law.
Alan Siddons 8/3/2009 23:58 :
Well, I’m sorry that you disagree, sir. As I said, it’s a simple
matter: prove me wrong. Take the previous back-radiation question. A
blackbody absorbing 1000 W/m² will, at 364 K, radiate 1000 in turn. So
if 50% is being re-radiated or reflected back to it, does one calculate
its "net outgoing emission" as 500 W/m² and does its temperature also
rise to 403 K? If, as you insist, 500 W/m² can indeed heat a 1000 W/m²
object, just tell me by how much.
All I’m asking for is a number, you see. Also please point me to an
empirical study which demonstrates that less intense radiation
transfers heat to a more energetic body. Otherwise I am forced to
conclude that the second law prevails and only a greater amount of
energy can heat it.
Or answer your own question. Say a 288 K body IS surrounded by a 200 K
universe. How much warmer will that body get?
I did the computation you want above . If it's totally
surrounded by 200K , it better come to 200k also , no matter how shade
or colored .
Brian Valentine
8/4/2009 10:38 :
Ooops, sorry for butting in, I had, to,
Looking
at your statement here Cork
“Do
you contend that your heated object will remain at the same temperature
as it
was?”
Cork,
you’re not suggesting that there are situations
for which heat is transmitted from cold -> hot, are
you?
Alan Siddons 8/4/2009 11:06 :
Howard,
I haven’t changed the
subject anywhere; I’ve merely addressed the points you raised.
1. The emissivity of
an entire planet cannot be assumed to be 1 after factoring in its
overall albedo. The method of estimating the earth’s temperature and
radiation budget is therefore faulty.
2. Back-radiation or
lesser radiation as a mechanism for raising an emitter’s temperature is
part of greenhouse-theory physics but not of real physics. Or, if it is an instance of real physics, I ask to
be shown.
So please don’t accuse
me of changing the subject, which implies that I’m being evasive. To
the contrary, I am charging headlong into it!
Your lab scenario is a
good one, a variation on my hot ball suspended inside an insulated
shell. And yes, I do contend that the hotter body (activated by
electrical resistance in this case) will transfer heat to its
surrounding shell while the shell won’t raise the hotter body’s
temperature. If radiation from the hot ball to the shell is greater
than what the shell is emitting, the shell will get warmer. If
radiation from each to the other is equal, neither body’s temperature
will rise. If radiation from the shell to the hot ball is greater than
what the ball is emitting, the ball will get warmer.
You see, I believe that
the concept of "radiative cooling" is a tricky one. Yes, a heated body
radiates. But by no means does this radiation compensate for the energy input. Rather, the
amount of radiation is simply a result of the temperature the input has
induced. That is to say, an input of energy vibrates that
body’s molecules, and this vibration produces an electromagnetic
disturbance which propagates through space. Confine that radiation like
a thermos does, though, and the heated body simply sustains the
temperature it has reached.
By direct
contrast, greenhouse physics contends that with a constant input of
energy (like sunlight), the suppression of outgoing radiation must
raise the body’s temperature because that body can only "cool off" by
radiating. Ergo, if outgoing energy is suppressed entirely, the input keeps pumping energy in and
the temperature rises inexorably. In this way a 1 watt input is capable
of producing the heat of a billion watts. THIS is the principle of
"radiative forcing" in a nutshell. And it’s nutty.
This false notion came
about because the founders of greenhouse theory misunderstood the
physics involved in their experiments. As you and I know, a high
interior temperature inside a glass box exposed to sunlight only occurs
because the enclosure suppresses convective cooling. But the founders
believed that glass was suppressing outgoing radiation (or
back-radiating it) and making incoming energy accumulate. Do you get
the idea? The founders thought that they were hindering radiative
cooling, which resulted in heating. The founders thought that they had
discovered a law of physics written in stone: Radiative disequilibrium
causes a temperature increase.
With a hop, skip, and a
jump, then, scientists started talking about the physics of suppressed
radiative cooling. If outgoing is 1 but back-radiation is ½, well gosh,
the temperature must rise, they insisted. Okay fine, I say. Just show
me the equation and tell me how MUCH the temperature rises. Show me the
physics.
Actually I just did above . Note Corky described
how clouds keep the ground warmer at nigh .
By the same token , they keep it cooler in the day time . Perhaps it's
because my background is much
stronger in statistics , but I am amazed that I have never seen the
notion of variance mentioned in any climate
discussion . While I won't know how much the spectrum of CO2 effects
the mean temperature of the planet until I
flesh out the spectum computation , it most certainly effects the rate
of both heating anc cooling by transferring energy back and forth with
the rest of the atmosphere . Over a cycle , its not unreasonable to
call this a reduction in variance .
Howard
Hayden 8/4/2009 11:50 :
Egad.
I am NOT -- repeat NOT -- suggesting any violation of the 2nd law of
thermodynamics.
I am saying with great certainty that IR WILL travel from the colder
body to the warmer, and will be absorbed by the warmer body.
That body will be warmer than if the cold body were replaced by empty
space that did not radiate heat back to the warmer body.
There are some interesting "paradoxes" in the non-equilibrium
thermodynamics about this very topic. One of them has two
bodies at equal temperature, with Radiant heat going back and
forth. One body becomes hotter than the other.
(It's all done with mirrors, but the physics is unassailable.)
Cheers,
Cork
Now this I'd like to see the physics of . That does violate
basic law .
Alan Siddons 8/4/2009 12:08 :
Whether radiatively or
conductively, a less energetic body (cooler) amplifying a more
energetic body (hotter) would violate the second law,
though.
For my part, I do think
it's possible that a zone can be made hotter with a mirror.
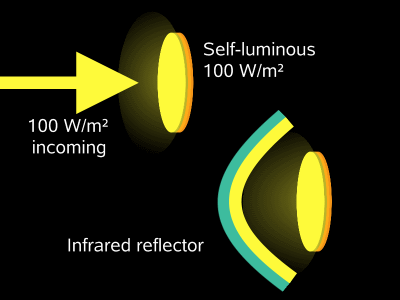
The temperature of a
self-luminous body exposed to radiation equal to what it is emitting
will NOT increase. But
focusing a reflected beam onto this self-luminous body will raise the
temperature of that zone. The atmosphere cannot be regarded as a
parabolic mirror, however.
Bob Ashworth 8/4/2009 12:09 :
Gentlemen:
The heated object will not remain at the same
temperature. It will
cool slower with insulation than it would if none were there.
Every
body in the universe radiates and absorbs energy constantly, but the
overall net heat transfer effect is always from the hotter to colder
body, never vice versa. That is it in a nutshell.
Pretty simple stuff.
Kindest Regards,
Bob
Peden HQ 8/4/2009 12:18 :

Bob Ashworth 8/4/2009 12:30 :
That sums it up - great visual! Use of a chicken is
very
appropriate for the AGWers are like Chicken Little (same size brains I
would expect) There cannot be any real scientists on the AGWers side,
by definition of what they say, charlatans maybe, scientists - no
way! It is a shame we even have to spend a second
of our time
fighting this play station crap!
Kindest Regards,
Bob
Alan Siddons 8/4/2009 12:32 :
Agreed, Bob.
However, if the emitter has a constant
energy supply (as does the Kiehl-Trenberth earth model with 235 watts
per square meter constantly radiating on it), it will not cool off at
all. Neither will a lesser magnitude of energy via reflection or
back-radiation RAISE its temperature because less cannot transfer heat
to more. Thermal energy keeps moving outward from that body,
never backward. I think you agree.
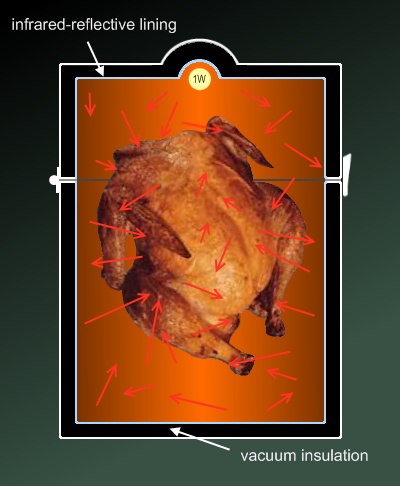
Alan Siddons 8/4/2009 12:32 :
This
is little more than a second version of Jim's oven
(always steal from the best), but mine has a
few touches that make it a better buy.
This
one’s insulated and firmly sealed like a thermos, for instance, and has
a quick-start radiation source, a battery-operated flashlight
bulb that makes it convenient for family camping. A double-A
Duracell will do. Principle of operation: Radiant energy goes in but
cannot get out. Greenhouse physics dictates that without an avenue of
exit, incoming photons accumulate and generate more and more
heat. Ergo, cut off exiting radiation entirely and you've got the
cheapest oven imaginable. Never overcook, though. The thing is
liable to melt.
I think all the stuff you are talking about is the epicycles
the AGWers use to compensate for their AE^%4 deficit .
I've pointed out that by their incorrect equation , they could make a
cyrogenic cooler just by coating the inner chamber
of a vacuum bottle with MgO .
Howard Hayden 8/4/2009 17:44 :
All:
Attached is a drawing for you. It's a
test.
G & T make a good point that the earth's
surface in full sunlight cannot be understood by moronic application of
the Stefan-Boltzmann law. Such an application ignores thermal
conductivity, heat capacity, evaporation, convection, directionality,
and all sorts of stuff that wind up with the surface much cooler than
the moronic application would suggest.
It is obvious that Stefan-Boltzmann combined with Kirchhoff explains
all but a few
percent of the temperature of the planet . How can that possibly be
denied ? How can it possibly
be denied that ignoring Kirchhoff and using equations which assign an
absorptivity of .7 to the earth and
an emissivity of 1.0 is simply wrong . How far off is 280k ?
All of the atmospheric processes
you mention work furiously to make the lumped system stay in balance
with its radiant bath .
I've made absolutely no denial of various forms of storage in the
system . But , damn it ,
you have to start with the correct equation and when you leave
Kirchhoff out , it is simply
wrong .
My quarrel was and is that the missive that came my
way had two errors of physics. It said that IR
cannot be radiated from a colder body to a hotter body, and that a grey
body (for sunlight) must be also a gray body (not a blackbody) in the
IR.
Again I will repeat that I am working on the full spectrum equation . I
am
not denying the effect of spectrum but I won't be happy until I'm
calculating it , not just
word waving .
Cheers,
Cork
------------
Howard Hayden
corkhayden@comcast.net
The Energy Advocate
www.energyadvocate.com
A Primer on CO2 and Climate, Second Edition ($14.95)
now available at
Vales Lake Publishing, LLC.
www.valeslake.com
PO Box
7609 * NEW P.O. NUMBER *
Pueblo West CO 81007
(fax) (719) 547-7819
People will do anything
to save the world ... except take a course in science.
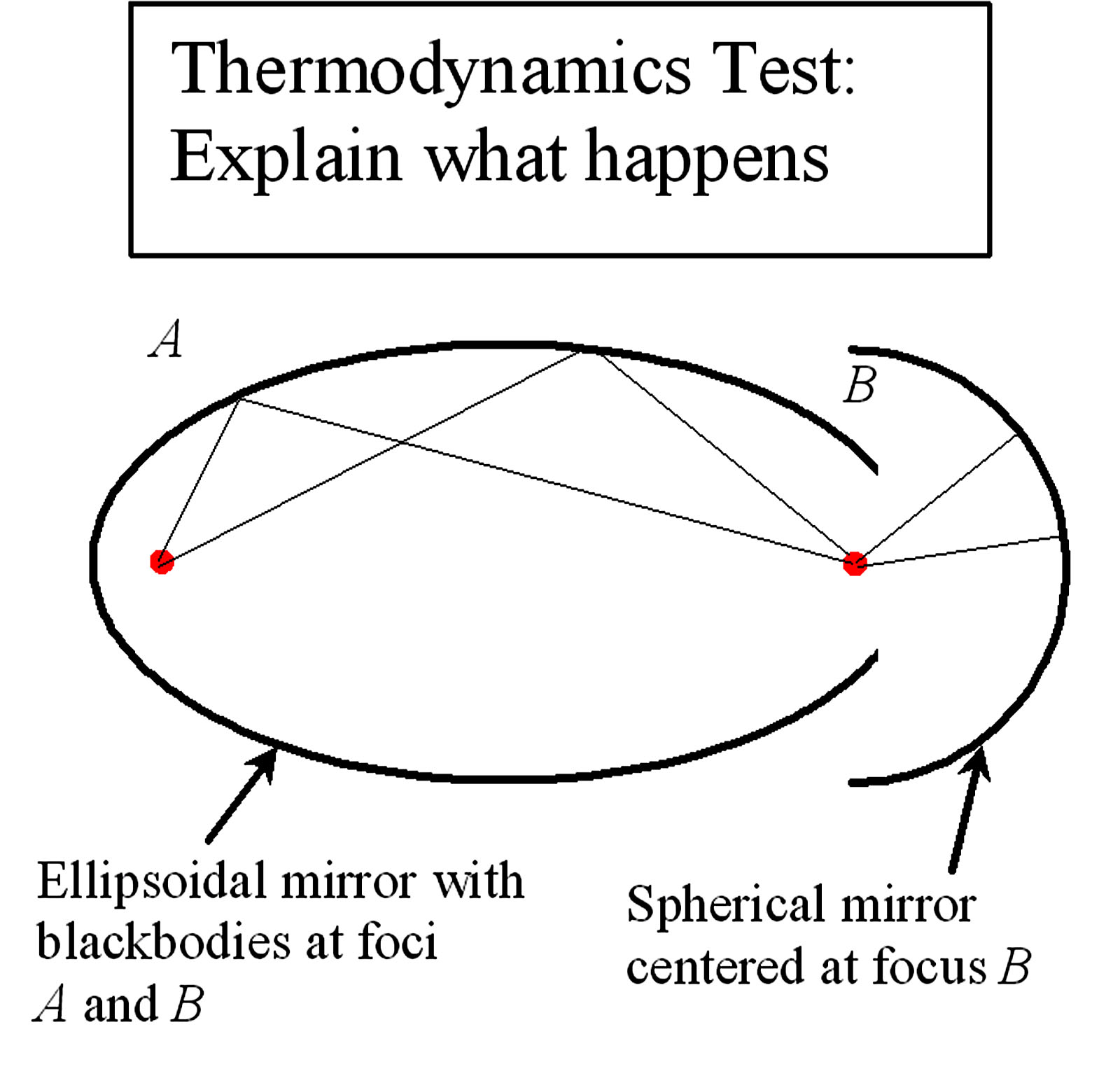
I'd like to see the explanation . Is the claim that you
can make a perpetual heat engine ?