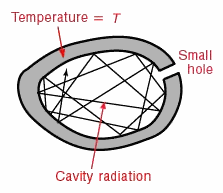
It's good to see Hertzberg discuss the "Cold Earth Fallacy" .
I think the fact that I have spent my life in the most powerful computing notations in the most effective computational notebook environments I could construct has virtually forced me into this battle . At this point , it seems crude to be discussing A and E as simple scalar averages when any change in ratio must be due to change in spectral correlation with sources and sinks , IE , changes in color .
I am really getting to dislike the use of energy rather temperature as everybody's input . It suppresses the essential spherical geometry . It suppresses the fact that we are heated by less than one millionth of the total sky @ ~ 6000k . Any sort of angular arrangement of AE can already be calculated with the current implementation . I'd love to see somebody else extend the radial dimension . Spectrum is my top priority .
--
Got to get to writing my next Serf City Logic of Liberty column .
I'll be getting to NYC , Oct 3-4 for The Singularity Summit 2009 .
alan618034 wrote:
I've been quite impressed by your facility at creating images . So you're an artist ? What software are you using ?Bob,
You have a true fix on me, I admit. Former radiochemist but I'€™m self-taught. Have done some tutoring in chemistry and college-level mathematics only because I learned these subjects myself, having no tolerance for schooling. I did well in naval medical training and art school, however. From portrait drawing you learn that it'€™s best to start with the basics, the main outline, the big picture, and then fill in the details. Do it backwards and you mess it all up. That'€™s how people mess up physics too, I feel.
That's a good description of the necessary progression of That's a good description of the necessary progression of mathematical sciences .
??? I don'€™t know why you mentioned Atlas Shrugged.
On blackbodies, I think it'€™s important to stress that the original blackbody set-up
mimics the very conditions that greenhouse physics says will raise an object'€™s temperature far above what'€™s expected (although you will never find a formula for it). Light goes in but can'€™t get out and is continuously back-radiated. Experiment shows, however, that this absence of radiative LOSS has no progressive heating effect. A radiatively restricted body will simply rise to the temperature of a blackbody exposed to the same amount of light because a blackbody IS a radiatively restricted body. Always citing blackbodies, greenhouse theorists smugly presume they'€™re following blackbody standards, graybodies too. In fact, their theory contradicts those standards.
Since you'€™re way beyond my level of expertise, I really don'€™t know what advice to offer. All I can say is to keep working on and thinking about it. An obsessed mind eventually finds a way to simplify. Here'€™s a Cro-Magnon sizing up a mammoth herd: "There'€™s this one and this one and this one and this one and this one and that one.... OH! There'€™s SIX!"
Most of the fundamental ideas of science are essentially simple, and may, as a rule, be expressed in a language comprehensible to everyone. '€” Albert Einstein
Alan
----- Original Message -----From: Bob ArmstrongTo: alanSent: Thursday, August 20, 2009 14:51Subject: Re: Can you point out anything I've said that's wrongAlan , I must admit to being curious about your background . It seems you have substantial commonsense instincts , but have not had a technical education . Any computing ?
alan618034 wrote:I think the intended point of Howard's paradox is that it supposedly sets up a situation energy will continuously flow from one point to another with no bound . In the case of a parabolic mirror , think of it chopped off somewhere this side of infinity and capped with a surface at some temperature . Then the flux passing thru the focus will match the flux radiating from that cap . [090820,1116 : alternatively , just consider the energy at that focus will match the energy missing from the mirror's shadow . ] The main thing I take from the discussion with Howard of his set up is that he has analyzed it to only the most superficial level .he appears to be one avoiding a concrete resolution
Yeah, not to disparage Hayden... but after I preemptively granted that a parabolic mirror could (or might) focus IR back to a heat emitter and raise a zone'€™s temperature without violating any law, he sent along that mirror example. And THEN accused me in a private email of avoiding the subject. I didn'€™t like that, especially since the subject is the presumed heating effect of an absorbing gas rather than a reflector. Does thermal energy, radiation included, conform to the second law or not? THAT is the question.
I've never read Atlas Shrugged and I've never seen Arrhenius's actual argument .In my view, the Achilles Heel of accepted climate theory (Arrhenius-based radiative "trapping") consists of starting with the valid premise that a blackbody absorbs all the radiation that falls upon it... then of adding the outrageous provision "including its own." I am a blackbody absolutist: A blackbody defines the upper limit of how much a physical substance'€™s molecules can vibrate in response to light, thereby radiating the same amount in turn. Redirecting this electromagnetism back to a blackbody cannot make its molecules vibrate any faster. Ergo, "back-radiation" won'€™t make a blackbody heat up.
I find your description of a black body something to think about . I think in some of your examples things get confused because you have energy sources on the inside of the surrounding insulation . In that case , the temperature will come to an equilibrium which will increase as as the insulation k , whether spectrally flat or not , increases . This is , due to radiation being radiated back to the source . In our case , assuming the heat from within the planet itself is way below our current precision of understanding , we are simply passively heated by the sun , and our mean energy density , temperature , ( oh , gee , I guess temperature itself is one of those meaningless means ! ) will come match that of its surroundings , which is one hot spot and a million times as large an area of near zero . The only shift in that mean will be if k is different in different directions . Note that in my implementation , in the homogeneous gray body case , I set the 0th element of AE , which corresponds to the disk of the sun to the same as the rest of the sky . An outgoing photon knows nothing about the density of incoming photons .I've never found the equations of radiative forcing . I find it a strange phrase . I guess they use it because , with their incorrect value for the equilibrium temperature of a gray body , any deviation from it must be a forcing . And what's to limit the magnitude of a forcing ?Which touches on my letter last night. From what I see, the concept of "radiative forcing" only exists because a valid method of determining planetary temperatures has never been devised. If a faulty and simplistic equation indicates that a planet should be cooler than it is, then, rather than question the equation, climatologists merely insert "forcing" to make up the difference. Yet the physics of forcing is unsound. Despite the fact that every planet with a substantial atmosphere is warmer than predicted (irrespective of that atmosphere'€™s contents), climatologists ignore this because they'€™re obsessed with the Arrhenius theory. That'€™s why I admire what you'€™re trying to do, start from scratch and let some fresh empirical air into the room.
Were it not for my experiences being kicked out of grad school thirty years ago , I wouldn't fathom how this obvious error could survive among any group which call themselves "climate scientists" . I would think the equations for the heat budgets of satellites would be exquisitely known and people from that community would have stopped the insanity .
Your profiles of the atmosphere are a major phenomenon to be understood . Even Feynman in his intro physics just describes the adiabatic cooling of the "exponential atmosphere' . But that's a future question as are such things as non-Lambertian radiation . ( I think the basic implementation works as well as it does because all the radiation has to go somewhere and the functions just assign one "summary" number to each direction in the celestial sphere .
Yea , some fresh empirical air . What ever happened to experimental physics requiring less than 100k$ ? The resistance , from both sides , to the notion of pertinent experiments to resolve the theory is astounding .
Alan , I'd be quite interested in your comments on what would make my presentation of the implementation more accessible . It's unfortunate that my 4th.CoSy is not a mature functioning notation , and the most accessible free language it's been translated to , J , is arguably the most mathematically dense language yet devised .
Peace thru Freedom ,
--
-- Bob Armstrong -- CoSy.com -- 719-337-2733 --I reserve the right to post all communications I receive or generate to CoSy website for further reflection .
alan618034 wrote:
Fahrenheit ? That's a legacy system still used in only a few backwards countries , isn't it ?Since we've been discussing geometry and the earth's temperature, Bob, I thought I might offer a minor contribution.
As you know, the accepted estimate of the earth'€™s average temperature is the result of dividing irradiance by four. Thus, since the earth absorbs about 70% of the sunlight falling on it, you take 1366 watts per square meter and multiply by 0.7. This yields 956. Now, because a sphere has four times the surface area of a disk, you divide 956 by four to get 239. So the earth'€™s temperature is believed to correspond to a blackbody exposed to 239 watts per square meter, i.e., 255 Kelvin, or minus 1'° Fahrenheit.
I actually don't remember seeing the %4 derivation , but I don't see that causing the error . It produces the same numbers my approach starting simply with the estimated solar temperature and the geometry . The obvious error is taking that 0.7 absorptivity and acting as if that did not equally affect the emission of the planet . That produces 279 - 255 = 24c of the deficit between the measured planet's temperature and the calculated .
BTW , I'd really like some best estimates of what the planet and the sun's mean temperature are observed to be .
Actually , means are quite affected by extreme values . But , of course , it is just the 0th term in any descriptive expansion .Is this a silly method for arriving at an average temperature? Yes. For one thing, this supposed "average" contains no information about highs and lows and in-betweens. It is devoid of specifics. Sunlight beaming directly down on this sphere at noon, for example, would induce a temperature of 189'° F, 190 degrees higher than the average. And what would be the lowest temperature on this body? Nobody knows because nobody CAN know through such a method.
Without the 4th root of .7 factor you get 394k instead of your 360 .
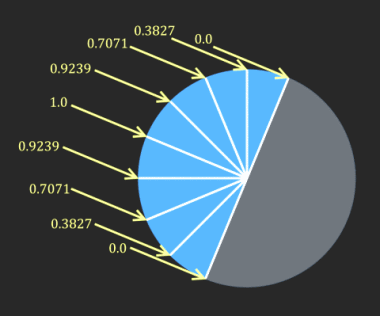
Although you can try guessing a temperature the "right" way, that is, by using trigonometric functions to determine irradiance on every point of a hemisphere,
you still end up knowing only the sunlit hemisphere's temperature and not that of the one in shadow.
In short, the problem is at least very difficult, if not unsolvable, as Gerlich and Tscheuschner have pointed out. But I do wish to discuss a detail I uncovered during my own struggles. I mentioned that at solar zenith the temperature would climb as high as 189'° on a model blackbody earth exposed to 956 W/m'². What about the average noon temperature along the entire meridian, then? That is partly solvable, and here'€™s how.
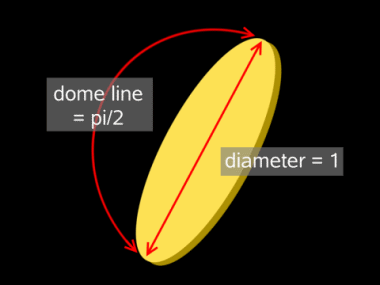
Taking a disc'€™s diameter as 1, its circumference will of course be pi. Mentally slice that circumference in half, "hinge" it upright to a vertical position, and the length of that line is therefore 1.57 compared to the diameter. Now, light that'€™s projected onto this ever-receding line is diminished due to the greater length it has to cover. If light shining directly on a flat disk has a strength of 1, then, the same light on the meridian is 1 divided by 1.57, i.e., the reciprocal of pi/2. This number is 0.6366, so 956 W/m'² falling along a noon meridian therefore has an effective strength of 608.6 watts per square meter, which corresponds to an average temperature of 120'° F! Or should in theory.
I was surprised by such a high temperature myself. And let me add that this 1/(pi/2) rule for a meridian occurred to me only because calculations with very tiny degree increments kept coming closer to a 0.6366 average sine. But one reason for this unexpected value pertains to the 4th root relationship between light and temperature.
 
Although the temperature at high latitudes falls off steeply, you'll notice, lower latitudes along a meridian are steadier than one might think: the earth'€™s overall temperature is "flatter" at solar noon than a semi-circle would suggest.
What I'm getting at is that if averaged irradiance is actually a valid method for obtaining a planet'€™s temperature (which I doubt), then dayside peak temperatures are the place to start. Temperature all goes downhill from there, of course, but how MUCH it falls as a physical planet rotates is a very complicated matter. From what I've surmised so far, however, there's no reason to believe that minus 1'° Fahrenheit for the earth has ever been a legitimate estimate.
Alan