Even on the realist side, the discussion always
sounds like the
Sun is just another "forcing" whose effect is still open to question.
Well, because the actual physics involved opens a can of worms
that
neither side of the debate is willing to deal with. This is why both
sides ignore Gerlich and Tscheuschner, for instance.
arguments as to why the [Stefan-Boltzmann] equation
doesn't
apply to earth (despite the fact that it clearly does).
Okay, here are a few. Assume that the method of dividing
irradiance
by four to obtain the temperature of a spherical, reflective Earth is
valid (although it isn’t). Thus, with 1366 watts per square meter
available but with 0.7 absorption, you divide by 4 and get 239 W/mē,
which, via Stefan-Boltzmann, corresponds to about 255 Kelvin on a
blackbody. The accepted method also assumes that this 255 K body will
then emit 239 W/mē. But Kirchhoff says it won’t, for emissivity is
equal to absorptivity. Given an absorptivity of 0.7, then, this
semi-smooth body at 255 K will emit 167 W/mē. Since it can’t absorb as
well as a blackbody, it can’t emit as well either. In short, the
accepted method of obtaining the Earth’s base temperature incorporates
absorptive but not emissive reduction. No body radiates as efficiently
as a blackbody. This means that a graybody necessarily retains its heat
longer than a blackbody, which thereby invalidates the initial 255 K
assumption, that of dividing irradiance by four.
The main thing I took away from a first browsing of
Gerlich and Tscheuschner
was Wood's 1909 experiment . They get too detailed too quickly
to answer my questions . Let me understand the lumped system , looking
at our 6370 + ~ 100 atmosphere km sphere as a whole , before getting
into
details . Thus by Stefan-Boltzmann/Kirchhoff only it's
spectrum as seen from the outside that determines its temperature as a
whole . Let's get that algorithm correct first . And you confirm what I
found on Wikipedia that it is ubiquitous to ignore Kirchhoff's
fantastic insight 150 years ago this year that absorptivity and
emissivity are in fact a single parameter , AE ,
and treat planets as absorbing as a gray body but radiating as a black
body . This creates an error to the down side of AE ^ %
4 ( fourth root of AE
) . You confirm below that the temperature of every planet is
above this erroneous value . Are they in fact much closer to the black
body calculation ? It appears the earth is quite close thus
not immune to the correct classical physics which
holds for every other object in the universe . It seems
"climate science" is working with an incorrect null
hypothesis . I don't understand what the nature of the theory
can be after this other than epicycles attempting to get back to that
correct classical hypothesis .
An interesting attribute of array programming
languages is that geometry is not not specified beyond the shape of the
parameters . For instance , While an integral expresses a summation
over every minute piece of a domain which thereby thoroughly defines
the domain , with
finite arrays , one is more inclined to think in terms of large scale
partitions of the domain . Thus the variable SfeerPart
in my implementation just must satisfy 1
= +/ SfeerPart . The most complicated
partition I've used divides SfeerPart
into the solid angles of the nightside , the sun disk , and the dayside
minus the sun disk .
That partition of the celestial sphere is
matched with temperatures , Tcs , and Kirchhoff
parameters , AE , for each element .
Given the Stefan-Boltzmann law :
sb : 5.6704e-008
/ Stefan-Boltzmann constant in ( W % m ^ 2 ) % K ^
4
Psb : {[ T ] sb * T ^ 4 }
/
Stefan-Boltzmann Law . returns W % m ^ 2
,
the mean temperature of a gray ball can be
calculated by setting the sum of its radiance in each direction
PgrayBall
: { +/ AE * SfeerPart * Psb x } / total
radiated power from shaded gray ball
with the temperatures in each matching direction :
Tdif : { -/ PgrayBall @/: ( Tcs ; x ) }
/ Difference between celestial sphere & earth
That is , find scalar temperature ,T
, for the
ball , such that 0.0
= Tdif T . With respect to temperature , the
sphere is a point or heat-superconductor
instantaneously averaging its temperature in all directions
. It displays no storage . I thank Mike Day for translating
these expressions into Iverson and Hui's freely available J
and Dyalog's APL so anyone can elaborate the
partition as they wish , for instance , specifying grayness as a
function of latitude . Even at this level one can think of a
lot of predictions testable either thru experiment or data analysis .
I've seen the statement that the sun's temperature varies by only a ten
of a percent from max to min of its sun spot cycle . But we we're only
dealing with variations of a few tenths of a percent at most
in mean temperature .
I find it interesting that since power is simply
buried in the summation , I've never thought in terms of W%M^2 ,
just temperature . I think it useful to be able to state a fraction ,
determined completely by geometry , for the mean temperature of a
planet
heated just by the sun .
Moreover, whereas a blackbody radiates 100% of the thermal
energy
impinging on it, the maximum rate of heat loss, a real body has
internal conductivity, allowing it to store heat. This too skews
temperature estimates. The moon, for example, is considered an 89%
blackbody. 1366 times 0.89 thus yields 1216 W/mē, which corresponds to
about 383 Kelvin on a blackbody, which should be close to its
temperature at solar noon. Does the moon’s surface actually reach that
temperature, though? No. Because, as Apollo-era measurements indicated,
the moon’s regolith stores some of that heat and releases it later.
This chart shows the deviation between predicted and actual
lunar
surface temperatures throughout the moon’s one-month "day".
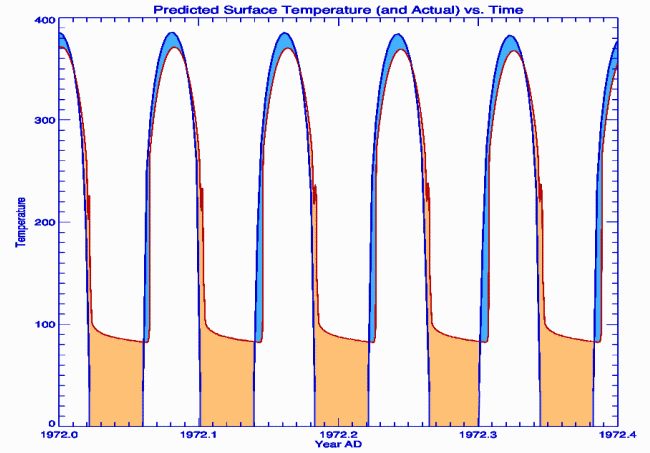
The blue zone depicts the moon's thermal handicap, the orange
its
advantage.
A real body exposed to the sun doesn’t heat up as fast as a
blackbody because it’s busy storing heat, conducting it internally into
itself rather than fully radiating it. So it never gets as hot. But
then it never gets as cold. Reaching its highest temperature in the
solar afternoon, it begins to
cool thereafter. And as it
does so, the stored heat below now creeps toward the surface. In
effect, a real body is a thermal battery. A blackbody has no such
attributes. And this gives the moon a higher than predicted average
temperature.
Your charts are great !
I absolutely agree that non-transparent mass acts
like a battery or capacitor . In fact , CO2 definitely a significant
role transferring heat back and forth to the atmosphere's more
transparent molecules . Storage changes the rate of heating
an cooling , but under what conditions can it change the mean over a
cycle ? Brian
Valentine raises this point . I've not looked at conductive
or convective heat dispersion so closely , but certainly Fourier's law
is symmetric . My intuition is that the sign of the derivative is
always in the direction of the equilibrium , it can't move that
equilibrium .
Yet the theory of the greenhouse effect was concocted for the
very
purpose of explaining why the earth in particular is warmer than
predicted.
As a final point, let me add that EVERY
planet is warmer than predicted by a divide-by-four
blackbody
formula.
As I have pointed out , It's not the divide by 4
that causes any error . It's the ignoring of Kirchhoff .
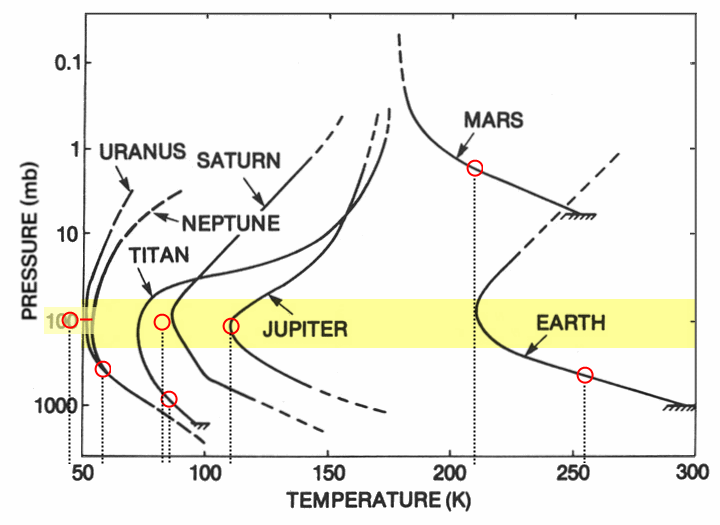
- 1. As one can see by the yellow band on this chart,
something happens to a planet's gases at pressures above a tenth
of a bar. In every case, air that had been getting cooler as
it
approached the planet now becomes progressively warmer, irrespective of
what it’s made of -- hydrogen, helium, nitrogen, carbon dioxide...
whatever.
- 2. Moreover, in every case it's apparent that air
temperature
would only keep rising if the planet itself (rake symbol) didn’t get in
the way. As its atmospheric pressure mounts, for instance, Jupiter
grows far hotter than Venus.
- 3. Finally, see how the heat lines extend beyond
the red
circles?
Each circle’s position refers to the temperature assigned to that
planet by the blackbody equation (see note). In every single case,
then, even for Mars, the actual temperature exceeds the estimate, i.e.,
the scientifically predicted temperature
for this
planet.
I find this a most interesting piece of data and two steps
beyond where I currently am in my understanding . I would first check
that all forms of energy including radiant and macro kinetic
are being accounted for . I assume charts like the above
refer to dayside profiles , not nightside . I want to repeat
again that at the application of the algorithm above is at the level of
the lumped planet and its atmosphere . It's only equating radiant
spectra between objects in space , not within the atmosphere . In a
sense , I am looking
at the radially lumped spectrum , but accounting for the the fact that
the ~ 6000k sun occupies less than a millionth of the total angular
area of the celestial
sphere. It is clear it accounts for the fact that we are ~ 300k . One
gedanken test for any theory is what does it predict if , instead of a
single hot spot like our sun , the temperature is constant over the
entire celestial sphere - like if the sun were gone and the radiant
temperature were 3k in all directions . Does the theory predict a
temperature for any object to be greater or less than 3k ? If
so , it is clearly broken .
Does the Stefan-Boltzmann equation apply to the Earth, then?
No.
There are too many other parameters (some perhaps unknown as yet) that
compromise its applicability. But does this significant discrepancy
bother so-called climate realists, let alone alarmists? No. In my view,
both sides of the radiative forcing debate are chasing their tails,
having never verified the initial assumptions of a theory they both
endorse. As you say, Bob, show me the physics.
Alan Siddons
Alan , Thank you enormously for such an informative
response .
As I've said above tho , nothing in the universe is
immune to Stefan-Boltzmann/Kirchhoff . And that missing 33k is created
by using a wrong equation , one which fails the gedanken experiment
above .
--
The next step in my understanding is implementing
the Planck function
Planck : {[ f ; T ] ( 2 * h * f ^ 3 ) %
c * ( _exp ( h * f ) % Boltz * T ) - 1 }
to generate black body spectra so that AE
can be expanded across spectra . While simply varying a spatially
uniform flat spectrum gray parameter does not change the equilibrium
temperature , a difference in the correlation of spectra between an
object and its radiant heat sources and sinks will . Then the actual
effect of various gas spectra can be computed .
At this point I would modify my challenge to Show
me the experimental physics .

